某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果 (千克),增种果树 (棵 ,它们之间的函数关系如图所示.
(1)求 与 之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量 (千克)最大?最大产量是多少?

现场学习题问题背景:在△ABC中,AB、BC、AC三边的长分别为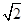 、
、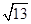 、
、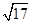 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.________
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为 、
、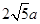 、
、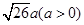 ,请利用图2的正方形网格(每个小正方形的边长为
,请利用图2的正方形网格(每个小正方形的边长为 )画出相应的△ABC,并求出它的面积是:.
)画出相应的△ABC,并求出它的面积是:.
探索创新:
(3)若△ABC三边的长分别为 、
、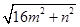 、
、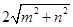
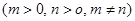 ,请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为:.
,请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为:.
某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
训练后篮球定时定点投篮测试进球数统计表:
| 进球数(个) |
8 |
7 |
6 |
5 |
4 |
3 |
| 人数 |
2 |
1 |
4 |
7 |
8 |
2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是,该班共有同学人;
(2)补全“训练前篮球定时定点投篮测试进球数统计图;
(3)训练后篮球定时定点投篮人均进球数.
如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.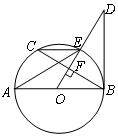
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,BC=2cm.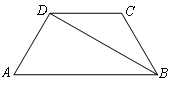
(1)求∠CBD的度数;
(2)求下底AB的长.
列方程(组)解应用题:
国家的“家电下乡”政策激活了农民购买能力,提高了农民的生活水平。“家电下乡”的补贴标准是:农户每购买一件家电,国家将按每件家电售价的13%补贴给农户.李大叔购买了一台彩电和一台洗衣机,从乡政府领到了390元补贴款.若彩电的售价比洗衣机的售价高1000元,求彩电和洗衣机的售价各是多少元.