如图,在 中, ,点 在 上, ,点 在 上,连接 , ,作 ,垂足为 .
(1)如图 ,当 时,连接 ,过点 作 交 的延长线于点 .
①求证: ;
②请猜想三条线段 , , 之间的数量关系,直接写出结论;
(2)如图 ,当 时,三条线段 , , 之间存在怎样的数量关系?请证明你的结论.
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
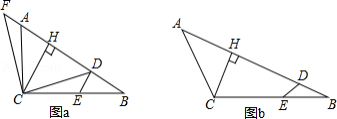
如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,
按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分?
(2)当t为何值时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP为等腰三角形?
小明是一名升旗手,面对高高的旗杆,他想出了好几种方法测量方法,学过直角三角形后,他只用一把卷尺就测出了旗杆AB的高度.下面是他测量的过程和数据:
第一步:测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1m(如图1),
第二步:拉着绳子的下端往后退,当他将绳子拉直时,测得此时拉绳子的手到地面的距离CD为1m,到旗杆的距离CE为8m,(如图2).他很快算出了旗杆的高度,请你也来试一试.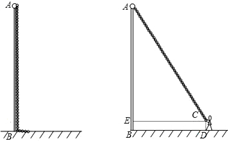
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠DEC=90°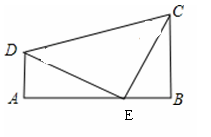
(1)△CDE是什么三角形?请说明理由
(2)若AD=6,AB=14,请求出BC的长.
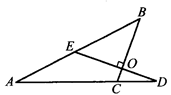
如图所示,BC⊥ED,垂足为O,∠A=27°,∠D=20°,求∠ACB与∠B的度数.