如图,已知二次函数 的图象交 轴于点 和点 ,交 轴于点 .
(1)求这个二次函数的表达式;
(2)若点 在第二象限内的抛物线上,求四边形 面积的最大值和此时点 的坐标;
(3)在平面直角坐标系内,是否存在点 ,使 , , , 四点构成平行四边形?若存在,直接写出点 的坐标;若不存在,说明理由.

已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.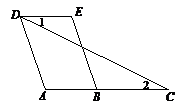
将求证:∠A=∠E 的过程填空完整.
证明:∵AD∥BE(已知),
∴∠A=(),
又∵∠1=∠2( 已知 ),
∴ED∥(),
∴∠E=(),
∴∠A=∠E().
在学习地理时,我们知道:“海拔越高,气温越低”,下表是海拔高度h(千米)与此高度处气温t(℃)的关系.
根据上表,回答以下问题.
(1)请写出气温t与海拔高度h的关系式;
(2)2014年3月8日,马航MH370航班失去联系,据报道称,马航MH370航班失去联系前飞行高度1066米,请计算在该海拔高度时的气温大约是多少?
(3)当气温是零下40℃时,其海拔高度是多少?
已知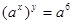 ,
,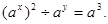
(1)求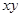 和
和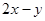 的值
的值
(2)求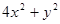 的值
的值
如图 是大众汽车的标志图案,其中蕴涵着许多几何知识.根据下面的条件完成证明.已知:如图,BC∥AD,BE∥AF.
是大众汽车的标志图案,其中蕴涵着许多几何知识.根据下面的条件完成证明.已知:如图,BC∥AD,BE∥AF.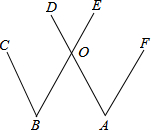
(1)求证:∠A=∠B;
(2)若∠DOB=135°,求∠A的度数.
先化简,再求值: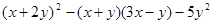 ,其中
,其中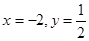 .
.