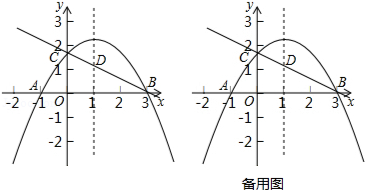
如图,在平面直角坐标系中,抛物线 (其中 、 为常数, 经过点 和点 ,且与 轴交于点 ,点 为对称轴与直线 的交点.
(1)求该抛物线的表达式;
(2)抛物线上存在点 ,使得 ,求点 的坐标;
(3)若点 为点 关于直线 的对称点,点 为直线 上一点,点 为坐标平面内一点,是否存在这样的点 和点 ,使得以 、 、 、 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
岳阳市的房价由前年的每平方米1800元涨到今年每平方米2592元,求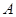 市的房价平均每年涨价百分之几?
市的房价平均每年涨价百分之几?
如图,已知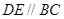 ,
,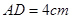 ,
,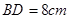 ,
,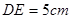 ,求线段
,求线段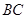 的长.
的长.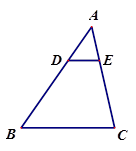
已知3是一元二次方程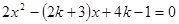 的一个根,求方程的另一个根及
的一个根,求方程的另一个根及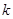 值.
值.
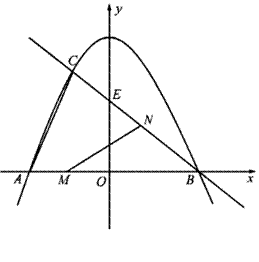
已知:如图,抛物线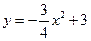 与
与 轴交于点
轴交于点 、点
、点 ,与直线
,与直线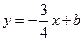 相交于点
相交于点 、点
、点 ,直线
,直线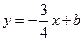 与
与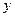 轴交于点
轴交于点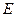 。
。
(1)求直线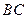 的解析式;
的解析式;
(2)求 的面积;
的面积;
(3)若点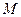 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从 向
向 运动(不与
运动(不与 重合),同时,点
重合),同时,点 在射线
在射线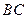 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从 向
向 运动.设运动时间为
运动.设运动时间为 秒,请写出
秒,请写出 的面积
的面积 与
与 的函数关系式,并求出点
的函数关系式,并求出点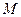 运动多少时间时,
运动多少时间时, 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
把两个全等的直角三角板ABC和EFG叠放在一起,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF的长均为4。
(1)当EG⊥AC于点K,GF⊥BC于点H时,如图23-1,求GH:GK的值.
(2)现将三角板EFG由图23-1所示的位置绕O点沿逆时针方向旋转,旋转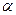 角满足条件:
角满足条件:
0°<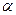 <30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.
<30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.
