某市为节约水资源，制定了新的居民用水收费标准，按照新标准，用-优题课

游客

题文

某市为节约水资源，制定了新的居民用水收费标准，按照新标准，用户每月缴纳的水费 $y$ （元 $)$ 与每月用水量 $x (m^{3})$ 之间的关系如图所示．

（1）求 $y$ 关于 $x$ 的函数解析式；

（2）若某用户二、三月份共用水 $40 m^{3}$ （二月份用水量不超过 $25 m^{3})$ ，缴纳水费 79.8 元，则该用户二、三月份的用水量各是多少 $m^{3}$ ？

科目数学题型解答题难度中等

知识点：一次函数的应用

登录免费查看答案和解析

相关试题

如图，在的正方形网格中，△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．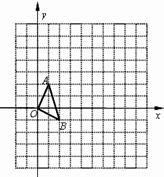

（1）以点O（0，0）为位似中心，按比例尺（OA︰OA’）1:3在位似中心的同侧将△OAB放大为△OA’B’，放大后点A、B的对应点分别为A’、B’ ．画出△OA’B’，并写出点A’、B’的坐标：A’（），B’（）；
（2）在（1）中，若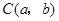为线段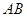上任一点，写出变化后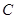点的对应点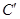的坐标（）．

解分式方程：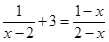

先化简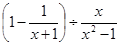：，再从不等式组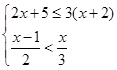的整数解中选择一个恰当的x值代入并求值．

如图1，已知有一张三角形纸片ABC的一边AB=10，若D为AB边上的点，过点D作DE//BC交AC于点E，分别过点D、E作DF⊥BC，EG⊥BC，垂足分别为点F、点G，把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠，点A、B、C分别落在A´、B´、C´处．若A´、B´、C´在矩形DFGE内或者其边上，且互不重合，此时我们称△A´B´C´（即图中阴影部分）为“重叠三角形”．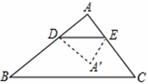

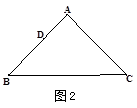
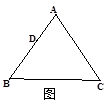
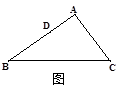
（1）实验操作：当AD=4时，①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，= ；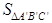
②若AB=AC，BC=12，如图3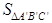，= ；③若∠B=30°，∠C=45°，如图4，= ；
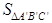（2）实验探究：若△ABC为等边三角形（如图5），设AD的长为m，若重叠三角形A´B´C´存在，试用含m的代数式表示重叠三角形A´B´C´的面积，并写出m的取值范围．

如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB_l∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB₁于F，G是EF中点，连结DG．设点D运动的时间为t秒．

（1）当t为何值时，AD=AB，并求出此时DE的长度；
（2）当△DEG与△ACB相似时，求t的值；
（3）以DH所在直线为对称轴，线段AC经轴对称变换后的图形为A′C′．当t>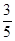时，连结C ′C，则以CC´为直径的圆何时与直线AB相切？

试卷网试题网古诗词网作文网范文网