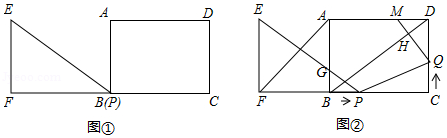
已知: 和矩形 如图①摆放(点 与点 重合),点 , , 在同一直线上, , , .如图②, 从图①的位置出发,沿 方向匀速运动,速度为 , 与 交于点 ;同时,点 从点 出发,沿 方向匀速运动,速度为 .过点 作 ,垂足为 ,交 于点 ,连接 , ,当点 停止运动时, 也停止运动.设运动时间为 ,解答下列问题:
(1)当 为何值时, ?
(2)设五边形 的面积为 ,求 与 之间的函数关系式;
(3)在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻 ,使点 在线段 的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.
(本小题8分)某商店购进一批冬季保暖内衣,每套进价为100元,售价为130元,每星期可卖出80套.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20套.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应该售价定为多少元?最大销售利润是多少?
(本小题6分) 如图,MN为半圆O的直径,半径OA⊥MN, D为OA的中点,过点D作BC//MN,
求证:( 1 ) 四边形ABOC为菱形; (2)∠MNB= ∠BAC
∠BAC
(本小题6分)
已知一抛物线与x轴的交点是 、B(1,0),且经过点C(2,8)。
、B(1,0),且经过点C(2,8)。
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标。
(本题6分)如图(第18题①),是日全食的初亏阶段,请用直尺和圆规作图,把图(第18题②)中的太阳补充完整.不写作法,但保留作图痕迹.
(本小题满分6分) 已知 与
与 成反比例,
成反比例,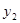 与
与 成正比例,并且当
成正比例,并且当 =3时,
=3时, =5,当
=5,当 =1时,
=1时, =-1;求
=-1;求 与
与 之间的函数关系式。
之间的函数关系式。