如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是()
A、1个 B、2个 C、3个 D、4个
李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( ,
,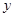 ),那么点P落在双曲线
),那么点P落在双曲线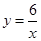 上的概率为()
上的概率为()
A.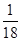 |
B.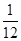 |
C.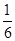 |
D.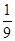 |
如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是()

如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC="3" cm,那么AE等于()
| A.3 cm | B. cm cm |
C.6 cm | D. cm cm |
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为()
A. |
B. |
C.4 | D.8 |