我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .
例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.
求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数 为“吉祥数”,求所有“吉祥数”;
(3)在(2)所得“吉祥数”中,求 的最大值.
正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.21教育网
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,-1),B(-5,-4),C(-2,-3)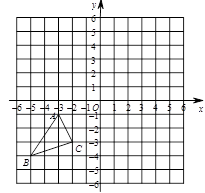
(1)作出△ABC向上平移6个单位,再向右平移7个单位的△A1B1C1。
(2)作出△ABC关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)将△ABC绕点O顺时针旋转900后得到△A3B3C3,请你画出旋转后的△A3B3C3
请在同一坐标系中画出二次函数① ;②
;② 的图象。说出两条抛物线的位置关系,指出②的开口方向、对称轴和顶点坐标及增减性。
的图象。说出两条抛物线的位置关系,指出②的开口方向、对称轴和顶点坐标及增减性。
解下列方程:
(1)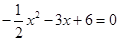
(2)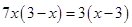
如图,点A是反比例函数 图像上的一点,过点A作AB⊥
图像上的一点,过点A作AB⊥ 轴于点B,且△AOB的面积为2,点A的坐标为
轴于点B,且△AOB的面积为2,点A的坐标为 .
.
(1)求m和k的值.
(2)若一次函数y=ax+3的图像经过点A,交双曲线的另一支于点C,交y轴于点D,求△AOC的面积.
(3)在 轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.