某学校为了解全校学生对电视节目的喜爱情况(新闻,体育,动画,娱乐,戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
如图1,要测一个小湖上相对两点A、B的距离,要求在AB所在直线同一侧岸上测.小明采取了以下三种方法,如图2,3,4.
(1)请你说明他各种测量方法的依据.
(2)根据所给条件求AB的长.
方法一:已知BC=50米,AC=130米,则AB=________米,其依据是_____________.
方法二:已知AO∶OD=OB∶OC=3∶1,CD=40米,则AB=____米,其依据是_____________.
方法三 :已知E、F分别为AC、BC的中点,EF=60米,则AB=________米,其依据是_____________.
如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=50米,你能知道小河的宽是多少吗?
如图,在四边形ABCD中,AC、BD相交于点O,∠ABD=∠ACD,试找出图中的相似三角形,并加以证明.
如图,正方形ABCD中,点E是CD的中点,点F在BC上,且CF∶BC=1∶4,你能说明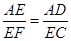 吗?
吗?
已知△ABC中,AB="15" cm,BC="20" cm,AC="30" cm,另一个与它相似的△A′B′C′的最长边为40 cm,求△A′B′C′的其余两边的长.