如图1，抛物线 过 、 两点，交 轴于点 ，过点 作 轴的平行线与抛物线上的另一个交点为 ，连接 、 ．点 是该抛物线上一动点，设点 的横坐标为 ．
（1）求该抛物线的表达式和 的正切值；
（2）如图2，若 ，求 的值；
（3）如图3，过点 、 的直线与 轴于点 ，过点 作 ，垂足为 ，直线 与 轴交于点 ，试判断四边形 的形状，并说明理由．
（本题7分）
一个不透明的袋中装有除颜色外都相同的球,其中红球13个,白球7个、黑球10个．
（1）求从袋中摸一个球是白球的概率；
（2）现从袋中取出若干个红球,放入相同数量的黑球,使从袋中摸出一个球是黑球的概率不超过40%,问至多取出多少个红球?
(本题8分）如图所示，正方形网格中的每个小正方形边长都是1，每个小格顶点称为格点，请以格点为顶点，在图甲、图乙中画出两个不全等但面积都是16的菱形．
（本题10分）
（1）计算：（-2015）0 ×|－3|－32+
；
（2）解方程：
－
= 2．
二次函数
的图象经过点（﹣1，4），且与直线
相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；
（3）在（2）的条件下，点N在何位置时，BM与NC相互垂直平分？并求出所有满足条件的N点的坐标．
如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．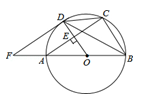
（1）求证：FD是⊙O的一条切线；
（2）若AB=10， AC=8，求DF的长．