知识背景
当 且 时,因为 ,所以 ,从而 (当 时取等号).
设函数 ,由上述结论可知:当 时,该函数有最小值为 .
应用举例
已知函数为 与函数 ,则当 时, 有最小值为 .
解决问题
(1)已知函数 与函数 ,当 取何值时, 有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为 天,则当 取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
如图①,在平面直角坐标系中,等腰直角△AOB的斜边OB在x轴上,顶点A的坐标为(3,3),AD为斜边上的高.抛物线y=ax2+2x与直线y=x交于点O、C,点C的横坐标为6.点P在x轴的正半轴上,过点P作PE∥y轴,交射线OA于点E.设点P的横坐标为m,以A、B、D、E为顶点的四边形的面积为S.求OA所在直线的解析式
求a的值
当m≠3时,求S与m的函数关系式.
如图②,设直线PE交射线OC于点R,交抛物线于点Q.以RQ为一边,在RQ的右侧作矩形RQMN,其中RN=.直接写出矩形RQMN与△AOB重叠部分为轴对称图形时m的取值范围.

情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是,∠CAC′=°.
问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=" k" AE,AC=" k" AF,试探究HE与HF之间的数量关系,并说明理由.
某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
|

 所表示的数分别为:
所表示的数分别为: ;
;
如图,某县城A距东西走向的一条铁路(图中DE)10km,县政府为改善城市人居环境,决定将城内一化工厂迁至距县城50km,方位为它的北偏东53o的B处(新厂址)。求搬迁后的化工厂到铁路的距离;
为方便县城居民和搬迁后化工厂货物运输,决定新修一个火车站C和一条连接县城、火车站、化工厂的公路,问火车站C修在直线DE的什么地方,使所修公路最短?并在图中作出点C的位置(保留作图痕迹,不要求写作法和证明)。(参考数据:sin53o≈0.8, cos53o≈0.6, sin37o≈0.6, cos37o≈0.8)

注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.如图①,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
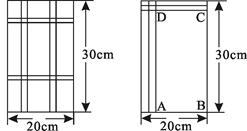
分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为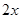 ,则每个竖彩条的宽为
,则每个竖彩条的宽为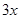 .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形 .
.结合以上分析完成填空:如图②,用含
 的代数式表示:
的代数式表示: =____________________________cm;
=____________________________cm; =____________________________cm;
=____________________________cm;
矩形 的面积为_____________cm
的面积为_____________cm ;
;
列出方程并完成本题解答.