将矩形 绕点 顺时针旋转 ，得到矩形 ．
（1）如图，当点 在 上时．求证： ；
（2）当 为何值时， ？画出图形，并说明理由．
如图，在△ABC中，∠B=∠C，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F．求证：
（1）△BDE≌△CDF；
（2）当△ABC是直角三角形时，试判断四边形AEDF的形状．
解方程：（1）
（用配方法）；（2）
计算或化简求值：
（1）计算：
；（2）化简求值：
，其中x=
．
数学游戏题：
（1）下图是一个三阶幻方，有9个数字构成，并且每横行，竖行和对角线上的3个数字的和都相等，试填出空格中的数；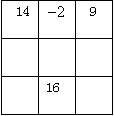
（2）有一种“二十四点”的游戏（即算24游戏），其游戏规则是这样的：任取四个1至13之间的自然数，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其结果等于24.例如对1，2，3，4，可作如下运算：(1+2+3)×4＝24（上述运算与4×(1＋2＋3)视为相同方法的运算）
①给出有理数4，6，9，12 ；请你写出一个算式使其结果为24；
②在我们学过负数以后这个游戏仍可以玩，如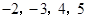
可以列出算式
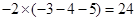；现给出
四个数，请你写出一个算式使其结果为24.
按如图所示的程序计算，若开始输入的x的值为48，我发现第一次得到的结果为24，第二次得到的结果为12，…，请你探索：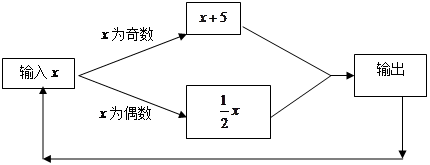
（1）第四次得到的结果；（2）第九次得到的结果；（3）第2012次得到的结果．