某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率 .
解不等式组 ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
化简求值: ,其中
,其中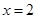 .
.
在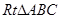 中,
中, ,
, ,
,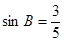 ,⊙
,⊙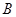 的半径长为1,⊙
的半径长为1,⊙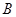 交边
交边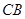 于点
于点 ,
,
点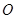 是边
是边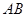 上的动点.
上的动点.
(1)如图1,将⊙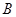 绕点
绕点 旋转
旋转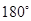 得到⊙
得到⊙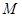 ,请判断⊙
,请判断⊙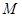 与直线
与直线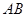 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求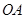 的长;
的长;
(3)如图3,点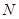 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙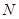 和以
和以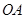 为半径的⊙
为半径的⊙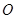 外切,设
外切,设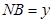 ,
, ,求
,求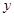 关于
关于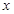 的函数关系式及定义域..
的函数关系式及定义域..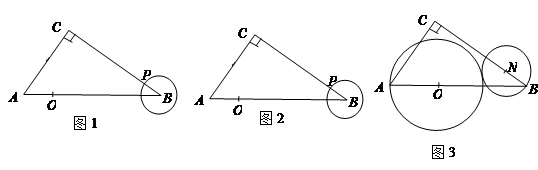
函数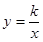 和
和
 的图像关于
的图像关于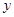 轴对称,我们把函数
轴对称,我们把函数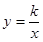 和
和
 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数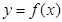 和
和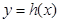 的图像关于
的图像关于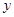 轴对称,那么我们就把函数
轴对称,那么我们就把函数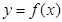 和
和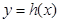 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数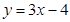 的“镜子”函数:,
的“镜子”函数:,
(2)函数的“镜子”函数是 ;
;
(3)如图7,一条直线与一对“镜子”函数 (
(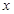 >
>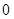 )和
)和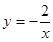 (
(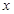 <
<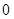 )的图像分别交于点
)的图像分别交于点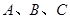 ,如果
,如果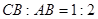 ,点
,点 在函数
在函数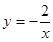 (
(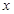 <
<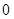 )的“镜子”函数上的对应点的横坐标是
)的“镜子”函数上的对应点的横坐标是 ,求点
,求点 的坐标.
的坐标.
如图6,在四边形 中,
中, ,
, 平分
平分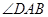 ,
,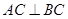 ,
,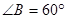 .
.
(1)求证:四边形 是等腰梯形;
是等腰梯形;
(2)取边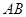 的中点
的中点 ,联结
,联结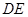 .求证:四边形
.求证:四边形 是菱形.
是菱形.