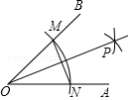
已知 ,求作 ,作法:
(1)以 为圆心,任意长为半径画弧分别交 , 于点 , ;
(2)分别以 , 为圆心,以 长为半径在角的内部画弧交于点 ;
(3)作射线 ,则 为 的平分线,可得
根据以上作法,某同学有以下3种证明思路:
①可证明 ,得 ,可得;
②可证明四边形 为菱形, , 互相垂直平分,得 ,可得;
③可证明 为等边三角形, , 互相垂直平分,从而得 ,可得.
你认为该同学以上3种证明思路中,正确的有
A.①②B.①③C.②③D.①②③
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线 上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是()
上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是()
A.( , , ) ) |
B.( , , ) ) |
C.( , , ) ) |
D.( , , ) ) |
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是()
A. m m |
B. m m |
C. m m |
D.1m |
如图.,C,D分別是线段AB,AC的中点,分别以点C,D为圆心, BC长为半径画弧,两弧交于点M,测量 的度数,结果为()
的度数,结果为()
| A.800 | B.900 | C.1000 | D.1050 |
已知⊙P的半径为2,圆心在函数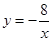 的图象上运动,当⊙P与坐标轴相切于点D时,则符合条件的点D的个数为()
的图象上运动,当⊙P与坐标轴相切于点D时,则符合条件的点D的个数为()
| A.0 | B.1 | C.2 | D.4 |
如图,已知点A是双曲线 在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为()
在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为()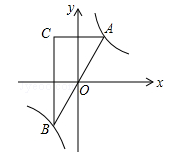
A.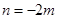 |
B. |
C. |
D. |