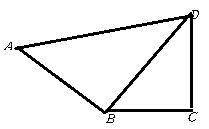
(1)数学理解:如图①, 是等腰直角三角形,过斜边 的中点 作正方形 ,分别交 , 于点 , ,求 , , 之间的数量关系;
(2)问题解决:如图②,在任意直角 内,找一点 ,过点 作正方形 ,分别交 , 于点 , ,若 ,求 的度数;
(3)联系拓广:如图③,在(2)的条件下,分别延长 , ,交 于点 , ,求 , , 的数量关系.

矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的_______相等;或者先证明四边形是菱形,在证明这个菱形有一个角是________ .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2,对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形.
如图1,矩形ABCD中,AB=6,BC=8,点E、F分别是BC、CD边上的点,且AE⊥EF,BE=2,
(1)求证:AE=EF;
(2)延长EF交矩形∠BCD的外角平分线CP于点P(图2),试求AE与EP的数量关系;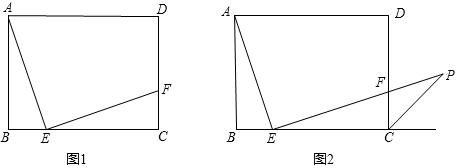
如图,已知 ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F。
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F。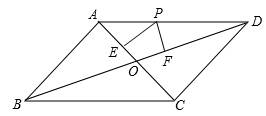
(1)若PF=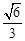 PE,PE=
PE,PE=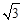 ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数;
(2)若点P是AD的中点,点F是DO的中点,PE=PF,BF=BC+ -4,求BC的长。
-4,求BC的长。
已知:如图, ,当
,当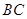 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.