某学校计划购买排球、篮球，已知购买1个排球与1个篮球的总费用为180元；3个排球与2个篮球的总费用为420元．
（1）求购买1个排球、1个篮球的费用分别是多少元？
（2）若该学校计划购买此类排球和篮球共60个，并且篮球的数量不超过排球数量的2倍．求至少需要购买多少个排球？并求出购买排球、篮球总费用的最大值？
新华书店推出售书优惠方案：一次性购书不超过100 元，不享受优惠；一次性购书超过100元但不超过200元一律打九折；一次性购书200元以上一律打八折．
（1）如果小明一次性购书的原价为250元，那么他实际付款_________元；
（2）如果小华同学一次性购书付款162元，那么小华所购书的原价为多少元？
如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．
（1）请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；
（2）若图中的正方形边长为2cm，长方形的长为3cm，宽为2cm，请直接写出修正后所折叠而成的长方体的体积：cm3．
化简求值：5a2＋3b2＋2(a2－b2)－(5a2－3b2)，其中
＋(b－
)2＝0．
解方程：（1）4－x＝2－3(2－x)；（2）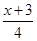
－
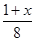＝1．
计算：（1）－2＋6÷(－2)×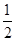
；（2）（－2）3－(1－
)×
．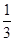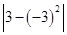