如图,抛物线 与 轴交于 、 两点, 点坐标为 ,与 轴交于点 .
(1)求抛物线的解析式;
(2)点 在 轴下方的抛物线上,过点 的直线 与直线 交于点 ,与 轴交于点 ,求 的最大值;
(3)点 为抛物线对称轴上一点.
①当 是以 为直角边的直角三角形时,直接写出点 的坐标;
②若 是锐角三角形,直接写出点 的纵坐标 的取值范围.

计算: .
某校为了解本校九年级学生足球训练情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级: 、 、 、 ,并将统计结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:

(1)补全条形统计图
(2)该年级共有700人,估计该年级足球测试成绩为 等的人数为 人;
(3)在此次测试中,有甲、乙、丙、丁四个班的学生表现突出,现决定从这四个班中随机选取两个班在全校举行一场足球友谊赛.请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.
荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
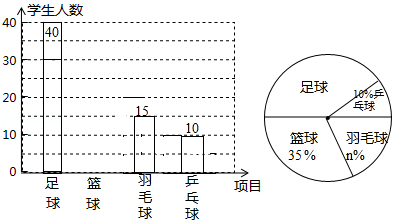
(1) , ;
(2)请补全图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球;
(4)在抽查的 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
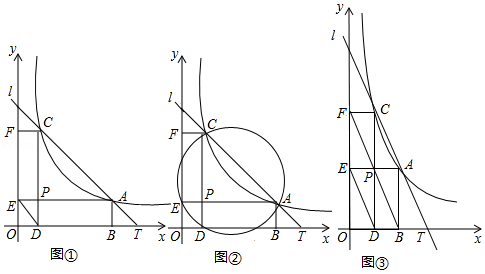
如图,直线 与函数 的图象相交于 、 两点,与 轴相交于 点,过 、 两点作 轴的垂线,垂足分别为 、 ,过 、 两点作 轴的垂线,垂足分别为 、 ;直线 与 相交于点 ,连接 .设 、 两点的坐标分别为 、 ,其中 .
(1)如图①,求证: ;
(2)如图②,若 、 、 、 四点在同一圆周上,求 的值;
(3)如图③,已知 ,且点 在直线 上,试问:在线段 上是否存在点 ,使得 ?如存在,请求出点 的坐标;若不存在,请说明理由.
在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.

(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.