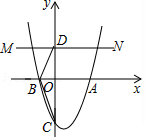
如图,在平面直角坐标系中,抛物线 与 轴交于点 、点 ,与 轴交于点 .
(1)求拋物线的解析式;
(2)过点 作直线 轴,点 在直线 上且 ,直接写出点 的坐标.
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.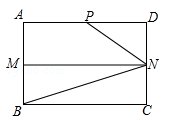
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大了建设资金的投入.
(1)机场建设项目中所有6个机场投入的建设资金金额统计如图1,已知机场E投入的建设资金金额是机场C,D所投入建设资金金额之和的三分之二,求机场E投入的建设资金金额是多少亿元?并补全条形统计图;
(2)将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表,根据扇形统计图及统计表中信息,求得a=,b=,c,d,m.(请直接填写计算结果)
现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ≈1.41,
≈1.41,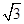 ≈1.73,结果保留整数)
≈1.73,结果保留整数)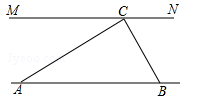
已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?