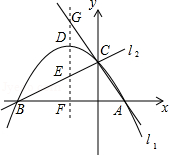
如图,已知两直线 , 分别经过点 ,点 ,且两条直线相交于 轴的正半轴上的点 ,当点 的坐标为 时,恰好有 ,经过点 、 、 的抛物线的对称轴与 、 、 轴分别交于点 、 、 , 为抛物线的顶点.
(1)求抛物线的函数解析式;
(2)试说明 与 的数量关系?并说明理由;
(3)若直线 绕点 旋转时,与抛物线的另一个交点为 ,当 为等腰三角形时,请直接写出点 的坐标.
为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
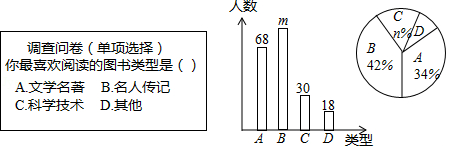
(1)本次调查共抽取了 名学生,两幅统计图中的 , .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“ ”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者 男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
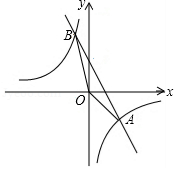
如图,已知 , 是一次函数 和反比例函数 的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求 的面积.
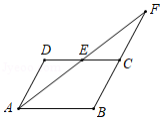
如图,点 是 的 边的中点, 、 的延长线交于点 , , ,求 的周长.
解分式方程: .
计算: .