如图1，在平面直角坐标系 中，抛物线 与 轴相交于 ， 两点，顶点为 ， ，设点 是 轴的正半轴上一点，将抛物线 绕点 旋转 ，得到新的抛物线 ．
（1）求抛物线 的函数表达式；
（2）若抛物线 与抛物线 在 轴的右侧有两个不同的公共点，求 的取值范围．
（3）如图2， 是第一象限内抛物线 上一点，它到两坐标轴的距离相等，点 在抛物线 上的对应点 ，设 是 上的动点， 是 上的动点，试探究四边形 能否成为正方形？若能，求出 的值；若不能，请说明理由．
小丽为了测旗杆AB的高度，小丽眼睛距地图1.5米，小丽站在C点，测出旗杆A的仰角为30o，小丽向前走了10米到达点E，此时的仰角为60o，求旗杆的高度。
11月读书节，深圳市为统计某学校初三学生读书状况，如下图：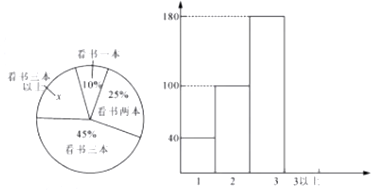
（1）三本以上的x值为，参加调差的总人数为，补全统计图；
（2）三本以上的圆心角为。
（3）全市有6.7万学生，三本以上有万人。
解方程：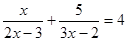
。
如图，过原点的直线
和
与反比例函数
的图象分别交于两点A，C和B，D，连结AB，BC，CD，DA．
（1）四边形ABCD一定是四边形；（直接填写结果）
（2）四边形ABCD可能是矩形吗？若可能，试求此时
和
之间的关系式；若不可能，说明理由；
（3）设P（
，
），Q（
，
）（
）是函数图象上的任意两点，
，
，试判断
，
的大小关系，并说明理由．
在Rt△ABC中，∠A=90°，AC=AB=4， D，E分别是AB，AC的中点．若等腰Rt△
绕点A逆时针旋转，得到等腰Rt△
，设旋转角为
，记直线
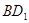与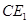
的交点为P．
（1）如图1，当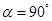
时，线段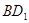的长等于，线段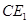的长等于；（直接填写结果）
（2）如图2，当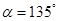
时，求证：
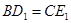,且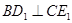
；
（3）①设BC的中点为M，则线段PM的长为；②点P到AB所在直线的距离的最大值为．（直接填写结果）