在Rt△ABC中，∠A=90°，AC=AB=4， D，E分别是AB，AC的中点．若等腰Rt△
绕点A逆时针旋转，得到等腰Rt△
，设旋转角为
，记直线
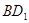与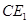
的交点为P．
（1）如图1，当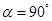
时，线段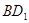的长等于 ，线段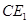的长等于 ；（直接填写结果）
（2）如图2，当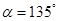
时，求证：
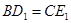,且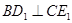
；
（3）①设BC的中点为M，则线段PM的长为 ；②点P到AB所在直线的距离的最大值为 ．（直接填写结果）
（本题8分）在数学课上，林老师在黑板上画出如图所示的图形（其中点B、F、C、E在同一直线上），并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2．
请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．
题设： ；结论： ．（均填写序号）
证明：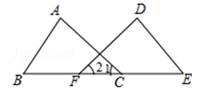
（本题8分）如图，B、C、E三点在同一条直线上，AC∥DE，AC＝CE，∠ACD＝∠B．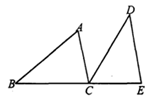
（1）求证：BC=DE；
（2）若∠A＝40°，求∠BCD的度数．
（本题5分）已知:如图，∠1＝∠2，∠C＝∠D，AD=EC，△ABD≌△EBC吗？为什么？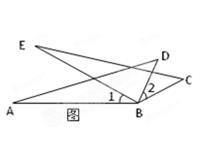
（本题5分）如图，AC⊥BC，AD⊥BD，垂足分别为C、D，AC=BD，Rt△ABC与Rt△BAD全等吗？为什么？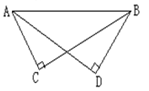
如图，阴影部分是由5个小正方形组成的一个直角图形，请用二种方法分别在下图方格内添涂黑二个小正方形，使阴影部分成为轴对称图形．