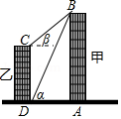
如图,线段 、 分别表示甲、乙两建筑物的高, , ,垂足分别为 、 .从 点测到 点的仰角 为 ,从 点测得 点的仰角 为 ,甲建筑物的高 米.
(1)求甲、乙两建筑物之间的距离 .
(2)求乙建筑物的高 .
解方程:
(1)
(2)
先化简,再求值: ,其中
,其中 .
.
如图,在平面内有A、B、C三点.
(1)画直线AC、线段BC、射线BA;
(2)画出△ABC的高CD,角平分线BE,中线AF
“利海”通讯器材市场,计划用60000元从厂家购进若干部新型手机,以满足市场需求.已知该厂家生产三种不一同型号的手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.
(1)若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完.请你帮助商场计算一下如何购买?
(2)若商场同时购进三种不同型号的手机共40部,并将60000元恰好用完,并且要求乙种型号的手机购买数量不少于6部且不多于8部,请你求出每种型号手机的购买数量.
某学校社会实践小分队走访100户家庭,发现一般洗衣水的浓度以0.2%-0. 5%为合适,即100kg洗衣水里含200-500g的洗衣粉比较合适,因为这时表面活性最大,去污效果最好.现有一个洗衣缸可容纳15kg洗衣水(包括衣服),已知缸中的已有衣服重4kg,所需洗衣水的浓度为0.4%,已放了两匙洗衣粉(1匙洗衣粉约为0.02kg)问还需加多少kg洗衣粉,添多少kg水比较合适?