如图①,在钝角 中, , ,点 为边 中点,点 为边 中点,将 绕点 逆时针方向旋转 度 .
(1)如图②,当 时,连接 、 .求证: ;
(2)如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;
(3)将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.

(本题8分)将下列各数化简后在数轴上表示出来:︱-1 ︱、︱0︱、-(-2)、绝对值是2的负数、-︱-3︱,并按从小到大的顺序将原数用不等号连接起来。
︱、︱0︱、-(-2)、绝对值是2的负数、-︱-3︱,并按从小到大的顺序将原数用不等号连接起来。
如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF。解答下列问题: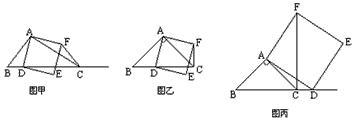
(1)如果AB=AC,∠BAC=90°。
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为,数量关系为;
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC>90°,点D在线段BC上运动.试探究:请直接写出当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外),不必说明理由。
(本题12分)在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,求证:△ABD≌△ACE.
(2)设∠BAC=α,∠BCE=β.
①如图1,当点D在线段BC上时,则α,β之间有怎样的数量关系?写出证明过程;
②当点D在直线BC上时,则α,β之间有怎样的数量关系?请画出图形并直接写出你的结论.

(本题10分)如图,设∠BAC= (0°<
(0°< <90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A
<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A 开始,用等长的小棒依次向右摆放,其中 A
开始,用等长的小棒依次向右摆放,其中 A A
A  为第一根小棒,且 A
为第一根小棒,且 A A
A =AA
=AA

(1)小棒能无限摆下去吗?答:.(填“能”或“不能”)
(2)若已经摆放了3根小棒,则 1 =,
1 =, 2=,
2=,  3=;(用含
3=;(用含 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求 的范围.
的范围.
(本题10分)已知,如图,四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,
求证:(1)MD=MB;(2)MN⊥BD