已知抛物线 与 轴交于 ， 两点， 为抛物线的顶点，抛物线的对称轴交 轴于点 ，连结 ，且 ，如图所示．
（1）求抛物线的解析式；
（2）设 是抛物线的对称轴上的一个动点．
①过点 作 轴的平行线交线段 于点 ，过点 作 交抛物线于点 ，连结 、 ，求 的面积的最大值；
②连结 ，求 的最小值．
图是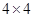
正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图4中黑色部分是一个中心对称图形.
如图所示,正方形网格中的每个小正方形边长都是1,画出一个周长为5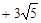
三角形,且使它的每个顶点都在小正方形的顶点上.判断你所画三角形的形状,并说明理由.
木工师傅为了让直尺经久耐用,常常在直尺的直角顶点与斜边之间加一个小木条,如下左图所示.下右图为其示意图.若∠BAC=90°,线段AB的长为5,线段AC的长为12,试求出小木条AD的最短长度.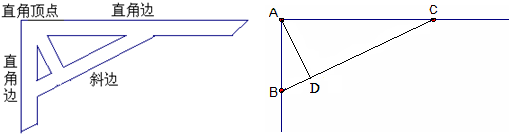
木工师傅做一个人字形屋梁,如图所示,上弦AB=AC=4m,跨度BC为6m,现有一根长为3m的木料打算做中柱AD(AD是△ABC的中线),请你通过计算说明这根木料的长度是否适合做中柱AD.(只考虑长度、不计损耗)
张老师在一次“探究性学习”课中,设计了如下表:
| n |
2 |
3 |
4 |
5 |
… |
| a |
22-1 |
32-1 |
42-1 |
52-1 |
… |
| b |
4 |
6 |
8 |
10 |
… |
| c |
22+1 |
32+1 |
42+1 |
52+1 |
… |
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n (n>1)的代数式表示:
a =" ______,b" =" ______,c" = ______.
(2)猜想:以a、b、c为边的三角形是否为直角三角形?并说明你的猜想.