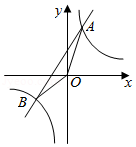
如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于 , 两点,且点 的坐标为 .
(1)求该一次函数的解析式;
(2)求 的面积.
如图1,在一直角边长为4米的等腰直角三角形地块的每一个正方形网格的格点(纵横直线的交点及三角形顶点) 上都种植同种农作物,根据以往种植实验发现,每株农作物的产量y(单位:千克) 受到与它周围直线距离不超过1米的同种农作物的株数x(单位:株) 的影响情况统计如下表:
| x(株) |
1 |
2 |
3 |
4 |
| y(千克) |
21 |
18 |
15 |
12 |
(1)通过观察上表,猜测y与x之间之间存在哪种函数关系,求出函数关系式并加以验证;
(2)根据种植示意图填写下表,并求出这块地平均每平方米的产量为多少千克?
| y(千克) |
21 |
18 |
15 |
12 |
| 频数 |
(3)有人为提高总产量,将上述地块拓展为斜边长为6米的等腰直角三角形,采用如图2所示的方式,在每个正方形网格的格点上都种植了与前面相同的农作物,共种植了16株,请你通过计算平均每平方米的产量,来比较那种种植方式更合理?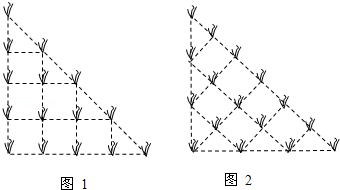
如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线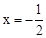

(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F;
求证:DF=DC.
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.