如图1,抛物线 与 轴交于 、 两点,与 轴交于点 ,已知点 坐标为 ,点 坐标为 .
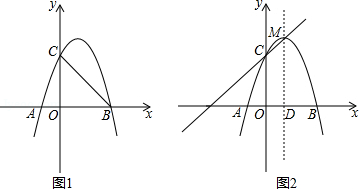
(1)求抛物线的表达式;
(2)点 为直线 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标;
(3)如图2,点 为该抛物线的顶点,直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.
以直线 为对称轴的抛物线
为对称轴的抛物线 与
与 轴交于A、B两点,其中点A的坐标为
轴交于A、B两点,其中点A的坐标为 .
.
(1)求点B的坐标;
(2)设点M 、N
、N 在抛物线线上,且
在抛物线线上,且 ,试比较
,试比较 、
、 的大小.
的大小.
一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,请你用列表或画出树状图的方法,求出两次摸出的球都是白球的概率.
如图,在离地面高度5米的C处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD(精确到0.01米).
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是;
(2)求△ABC与△A′B′C′的面积比.
解方程: