我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量 (百件)与时间 为整数,单位:天)的部分对应值如表所示,网上商店的日销售量 (百件)与时间 为整数,单位:天)的部分对应值如图所示.
时间 (天 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
日销售量 (百件) |
0 |
25 |
40 |
45 |
40 |
25 |
0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映 与 的变化规律,并求出 与 的函数关系式及自变量 的取值范围;
(2)求 与 的函数关系式,并写出自变量 的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为 (百件),求 与 的函数关系式;当 为何值时,日销售总量 达到最大,并求出此时的最大值.

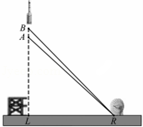
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面 处发射,当火箭达到 点时,从位于地面 处雷达站测得 的距离是 ,仰角为 ;1秒后火箭到达 点,此时测得仰角为
(1)求发射台与雷达站之间的距离 ;
(2)求这枚火箭从 到 的平均速度是多少(结果精确到 ?
(参考数据: , , , , ,
在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 ,乙成绩的平均数是 ;
(2)经计算知 , .你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
解不等式组: .
如图,已知抛物线 与 轴交于 、 两点,与 轴交于点
(1)求点 , , 的坐标;
(2)点 是此抛物线上的点,点 是其对称轴上的点,求以 , , , 为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点 ,使得 是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.

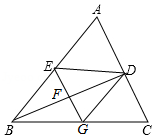
如图, 是 的角平分线,它的垂直平分线分别交 , , 于点 , , ,连接 , .
(1)请判断四边形 的形状,并说明理由;
(2)若 , , ,点 是 上的一个动点,求 的最小值.