在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点 垂直起飞到达点 处,测得1号楼顶部 的俯角为 ,测得2号楼顶部 的俯角为 ,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且 和 分别垂直地面于点 和 ,点 为 的中点,求2号楼的高度.(结果精确到
(参考数据 , , , , ,

若 无意义,且
无意义,且 ,求
,求 的值.
的值.
如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求点M、N,使PM+MN+NQ最短.
计算(4分+6分,共10分)
(1)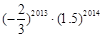 (2)
(2) 
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.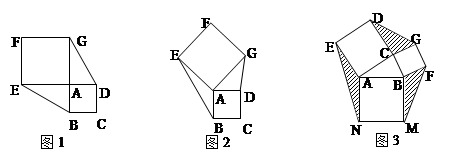
(1)发现:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积
关系是:.
(2)引申:当正方形AEFG旋转任意一个角度时(如图2),△ABE与△ADG的面
积关系是:______________________.并证明你的结论.
证明:
(3)运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图3),则图中阴影部分的面积和的最大值是cm2.
如图①,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN.延长MP交CN于点E(如图②).
(1)求证:△BPM≌△CPE;(2)求证:PM=PN.