在平面直角坐标系中，抛物线 与 轴交于点 、 ，交 轴于点 ，点 为抛物线的顶点，对称轴与 轴交于点 ．
（1）求抛物线的解析式；
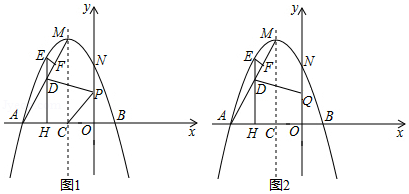
（2）如图1，连接 ，点 是线段 上方抛物线上一动点， 于点 ，过点 作 轴于点 ，交 于点 ．点 是 轴上一动点，当 取最大值时：
①求 的最小值；
②如图2， 点为 轴上一动点，请直接写出 的最小值．
画出△ABC关于原点对称的图形△DEF,并写出D、E、F的坐标.
先化简 (1+ 
)÷
，然后在0，1，－1中挑选一个合适的数代入求值．
解方程：（本题8分，每小题4分）
（1）
；
（2）
.
(本题满分12分)已知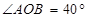
，∠AOB的余角为∠AOC，∠AOB的补角为∠BOD，OM平分∠AOC， ON平分∠BOD．
（1）如图，当射线OM在∠AOB的外部时，用直尺、量角器画出射线OD，ON的准确位置；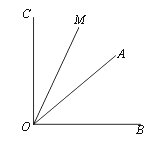
（2）求（1）中∠MON的度数，要求写出计算过程；
解：
(本题满分12分)现在，友谊商场进行促销活动，出售一种优惠购物卡（注：此卡只作为购物优惠凭证不能顶替货款），花300元买这种卡后，凭卡可在这家商场按标价的8折购物.
（1）顾客购买多少元金额的商品时，买卡与不买卡花钱相等？在什么情况下购物合算？
（2）小张要买一台标价为3500元的冰箱，如何购买合算？小张能节省多少元钱？
（3）小张按合算的方案，把这台冰箱买下，如果友谊商场还能盈利25％，这台冰箱的进价是多少元？