如图，反比例函数ykx(x<0)过点A(3,4)，直线AC与-优题课

题文

如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 过点 $A (3, 4)$ ，直线 $AC$ 与 $x$ 轴交于点 $C (6, 0)$ ，过点 $C$ 作 $x$ 轴的垂线 $BC$ 交反比例函数图象于点 $B$ ．

（1）求 $k$ 的值与 $B$ 点的坐标；

（2）在平面内有点 $D$ ，使得以 $A$ ， $B$ ， $C$ ， $D$ 四点为顶点的四边形为平行四边形，试写出符合条件的所有 $D$ 点的坐标．

科目数学题型计算题难度中等

知识点：反比例函数的性质待定系数法求反比例函数解析式平行四边形的判定与性质反比例函数综合题

登录免费查看答案和解析

相关试题

如图，在平面直角坐标系 $xOy$ 中，抛物线 $y = x^{2} - 2 x - 3$ 交 $x$ 轴于 $A$ ， $B$ 两点（点 $A$ 在点 $B$ 的左侧），将该抛物线位于 $x$ 轴上方曲线记作 $M$ ，将该抛物线位于 $x$ 轴下方部分沿 $x$ 轴翻折，翻折后所得曲线记作 $N$ ，曲线 $N$ 交 $y$ 轴于点 $C$ ，连接 $AC$ 、 $BC$ ．

（1）求曲线 $N$ 所在抛物线相应的函数表达式；

（2）求 $ΔABC$ 外接圆的半径；

（3）点 $P$ 为曲线 $M$ 或曲线 $N$ 上的一动点，点 $Q$ 为 $x$ 轴上的一个动点，若以点 $B$ ， $C$ ， $P$ ， $Q$ 为顶点的四边形是平行四边形，求点 $Q$ 的坐标．

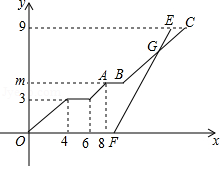
小强与小刚都住在安康小区，在同一所学校读书，某天早上，小强 $7 : 30$ 从安康小区站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留2分钟，校车行驶途中始终保持匀速，当天早上，小刚 $7 : 39$ 从安康小区站乘坐出租车沿相同路线出发，出租车匀速行驶，比小强乘坐的校车早1分钟到学校站点，他们乘坐的车辆从安康小区站出发所行使路程 $y$ （千米）与校车行驶时间 $x$ （分钟）之间的函数图象如图所示．

（1）求点 $A$ 的纵坐标 $m$ 的值；

（2）小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车？并求此时他们距学校站点的路程．

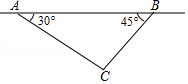
如图所示，飞机在一定高度上沿水平直线飞行，先在点 $A$ 处测得正前方小岛 $C$ 的俯角为 $30 °$ ，面向小岛方向继续飞行 $10 km$ 到达 $B$ 处，发现小岛在其正后方，此时测得小岛的俯角为 $45 °$ ，如果小岛高度忽略不计，求飞机飞行的高度（结果保留根号）．

先化简，再求值： $\frac{x}{x - 1} + \frac{x + 1}{x^{2} - 1}$ ，其中 $x = 2$ ．

计算： $| - 3 | + {(- 1)}^{4} - 2 \tan 45 ° - {(π - 1)}^{0}$ ．

试卷网试题网古诗词网作文网范文网