如图1,抛物线 与 轴交于点 和点 ,与 轴交于点 ,抛物线 的顶点为 , 轴于点 .将抛物线 平移后得到顶点为 且对称轴为直线 的抛物线 .

(1)求抛物线 的解析式;
(2)如图2,在直线 上是否存在点 ,使 是等腰三角形?若存在,请求出所有点 的坐标;若不存在,请说明理由;
(3)点 为抛物线 上一动点,过点 作 轴的平行线交抛物线 于点 ,点 关于直线 的对称点为 ,若以 , , 为顶点的三角形与 全等,求直线 的解析式.
(广元)如图,已知抛物线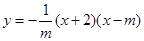 (
(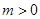 )与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
)与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
(1)若抛物经过点C(2,2),求实数m的值;
(2)在(1)的条件下,解答下列问题:
①求出△ABC的面积;
②在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,使得以点A、B、M为顶点的三角形与△ACB相似?若存在,求m的值;若不存在.请说明理由.
(绵阳)如图,反比例函数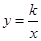 (
( )与正比例函数
)与正比例函数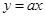 相交于A(1,k),B(﹣k,﹣1)两点.
相交于A(1,k),B(﹣k,﹣1)两点.
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数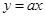 的图象平移,得到一次函数
的图象平移,得到一次函数 的图象,与函数
的图象,与函数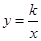 (
( )的图象交于C(
)的图象交于C(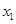 ,
,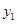 ),D(
),D(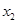 ,
, ),且
),且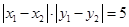 ,求b的值.
,求b的值.
(绵阳)南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1000元,乙货船每艘运费1200元.
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式;
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
(绵阳)已知抛物线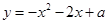 (
( )与y轴相交于A点,顶点为M,直线
)与y轴相交于A点,顶点为M,直线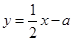 分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.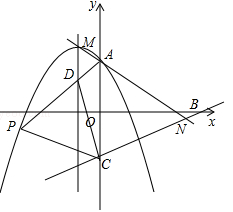
(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;
(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;
(3)在抛物线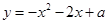 (
(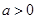 )上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(绵阳)如图,在边长为2的正方形ABCD中,G是AD延长线时的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.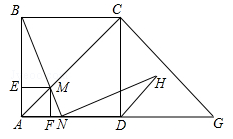
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.