在一次社会调查活动中,小李收集到某“健步走运动”团队20名成员一天行走的步数,记录如下:
5640 |
6430 |
6520 |
6798 |
7325 |
8430 |
8215 |
7453 |
7446 |
6754 |
7638 |
6834 |
7326 |
6830 |
8648 |
8753 |
9450 |
9865 |
7290 |
7850 |
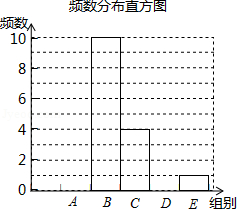
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表,步数分布统计图.
组别 |
步数分组 |
频数 |
|
|
|
|
|
10 |
|
|
4 |
|
|
|
|
|
1 |
根据以上信息解答下列问题:
(1)填空: , ;
(2)请补全条形统计图;
(3)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;
(4)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
如图11,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
(1)求证:AG=C′G;
(2)如图12,再折叠一次,使点D与点A重合,的折痕EN,EN角AD于M,求EM的长.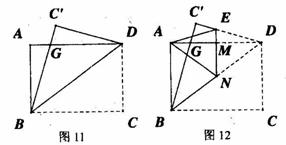
如图9,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图10,连接CE,⊙O的半径为5,AC长为4,求阴影部分面积之和.(保留∏与根号)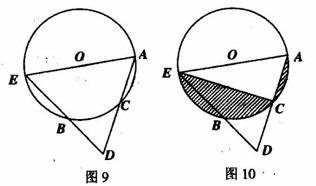
某校为了解本校八年级学生的课外阅读喜好,随即抽取部分该校八年级学生进行问卷调查(每人只选一种书籍),图8是整理数据后画的两幅不完整的统计题,请你根据图中的信息,解答下列问题
(1)这次活动一共调查了名学生.
(2)在扇形统计图中,“其它”所在的扇形圆心角为度.
(3)补全条形统计图
(4)若该校八年级有600人,请你估计喜欢“科普常识”的学生有人.
解分式方程: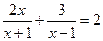
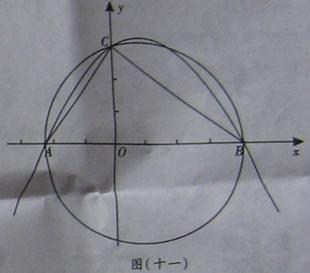
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.