如图11,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
(1)求证:AG=C′G;
(2)如图12,再折叠一次,使点D与点A重合,的折痕EN,EN角AD于M,求EM的长.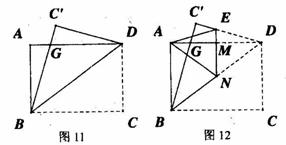
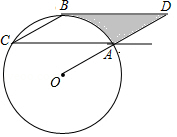
如图,点 、 、 在半径为8的 上,过点 作 ,交 延长线于点 .连接 ,且 .
(1)求证: 是 的切线;
(2)求图中阴影部分的面积.
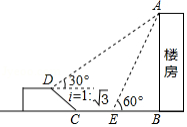
如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面 处测得楼房顶部 的仰角为 ,沿坡面向下走到坡脚 处,然后向楼房方向继续行走10米到达 处,测得楼房顶部 的仰角为 .已知坡面 米,山坡的坡度 (坡度 是指坡面的铅直高度与水平宽度的比),求楼房 高度.(结果精确到0.1米)(参考数据: ,
关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.
某学校为了丰富学生课余生活,开展了“第二课堂”的活动,推出了以下四种选修课程: .绘画; .唱歌; .演讲; .十字绣.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
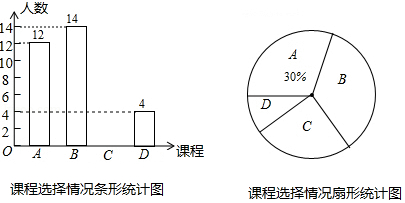
(1)这次学校抽查的学生人数是 ;
(2)将条形统计图补充完整;
(3)如果该校共有1000名学生,请你估计该校报 的学生约有多少人?