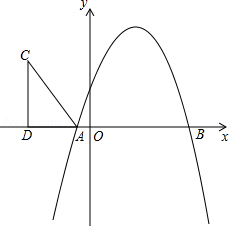
如图，抛物线 与 轴分别交于 ， 两点．
（1）求抛物线的解析式；
（2）在第二象限内取一点 ，作 垂直 轴于点 ，连接 ，且 ， ，将 沿 轴向右平移 个单位，当点 落在抛物线上时，求 的值；
（3）在（2）的条件下，当点 第一次落在抛物线上记为点 ，点 是抛物线对称轴上一点．试探究：在抛物线上是否存在点 ，使以点 、 、 、 为顶点的四边形是平行四边形？若存在，请求出点 的坐标；若不存在，请说明理由．
将下列各数填在相应的集合里。
—3.8，—10， 4.3，—∣—
∣， 42， 0，—（—
）
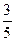整数集合：{… }；
分数集合：{… }；
正数集合：{… }；
负数集合：{… }。
气象资料表明，高度每增加1千米，气温大约下降6℃。
⑴我国著名风景区黄山的天都峰高1700米，当地面温度约为18℃时，求山顶气温。
⑵小明和小颖想出一个测量山峰高度的方法，小颖在山脚，小明在峰顶，他们同时在上午10点测得山脚和山峰顶的气温分别为22℃和7℃，你知道山峰高多少千米吗？
有理数
、
在数轴上对应点如图所示：
⑴在数轴上表示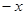
、
；
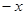⑵试把、、0、、这五个数从大到小用“＞”号连接起来．
小明的家（记为A）与他上学的学校（记为B），书店（记为C）依次座落在一条东西走向的大街上，小明家位于学校西边30米处，书店位于学校东边100米处，小明从学校沿这条街向东走40米，接着又向西走了70米到达D处，规定向东为正，试用数轴表示上述A、B、C、D的位置。
张金同学给自己的压岁钱记了流水账，大姑给+50元，二姑给30元，三叔给20元，去动物园花了10元，记为－10元，买文具用品花了15元，记为－15元，他的账上余额为多少元？