长清自来水公司为了鼓励节约用水，采取分段收费标准，若某户居民每月应交水费（y元）是用水量x（吨）的函数，其图象如图所示。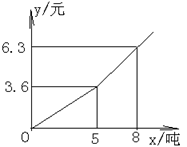 
分别写出x≤5和x＞5时，
y与x之间的函数解析式观察函数的图象，利用函数的解析式，
回答自来水公司采取的收费标准是：
答：_______________________________________________
_______________________________________________。若某户居民该月用水3.5吨，则应交水费____元；若该月交水费9元，则用水_______吨。
已知：抛物线C1：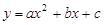
经过点A（-1，0）、B (3，0)、C（0，-3）．（1）求抛物线C1的解析式；
（2）将抛物线C1向左平移几个单位长度，可使所得的抛物线C2经过坐标原点，并求出C2的解析式；
|
（3）把抛物线C1绕点A（-1，0）旋转180°，求出所得抛物线C3的解析式．
如图，RtΔDBC中，∠DBC=90º，BG⊥DC，BA=BC=20，AC=32．求AD的长.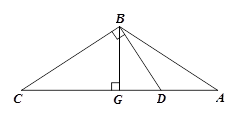
如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.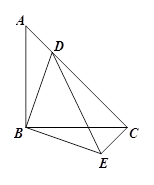
（1）求∠DCE的度数；
（2）当AB=4，AD∶DC=1∶3时，求DE的长.
如图，△ABC在方格纸中.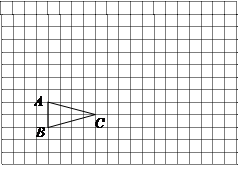
（1）请在方格纸上建立平面直角坐标系，使A（-5，-1），C（-1，-2），并求出
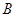点坐标；（2）以原点
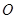为旋转中心，将△ABC绕点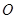逆时针旋转90º得到△A’B’C’.请在图中画出△A’B’C’，并写出点A’，B’，C’的坐标.（3）以原点
为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A’’B’’C’’.
已知：抛物线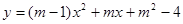
的图象经过原点，且开口向上.（1）确定
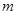的值；（2）求此抛物线的顶点坐标；
（3）画出抛物线的图象，结合图象回答：当
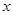取什么值时，
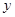随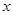的增大而增大？
（4）结合图象直接回答：当
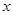取什么值时，
？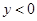