四川省安岳县盛产柠檬和柚子两种水果，今年，某公司计划用两种型号的汽车运输柠檬和柚子到外地销售，运输中要求每辆汽车都要满载满运，且只能装运一种水果．若用3辆汽车装载柠檬、2辆汽车装载柚子可共装载33吨，若用2辆汽车装载柠檬、3辆汽车装载柚子可共装载32吨．
（1）求每辆汽车可装载柠檬或柚子各多少吨？
（2）据调查，全部销售完后，每吨柠檬可获利700元、每吨柚子可获利500元，计划用20辆汽车运输，且柚子不少于30吨，如何安排运输才能使公司获利最大，最大利润是多少元？
受全球金融危机的影响,出现了大学毕业生就业难的问题,政府为了积极采取措施,需要掌握求职者求职情况.现对求职者进行抽样调查，若求职者每人都投出50张求职申请,根据“得到用人单位面视通知的次数”作统计，如下图.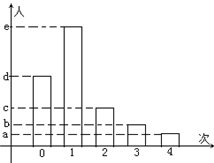
(1)样本中的众数是.
(2)如果a:b:c:d:e=2:3:5:8:12，样本容量是900，求中位数和没得到用人单位面视通知的人数.
(3)任意采访一个大学毕业生的求职者，求出他“至少得到一次用人单位面视通知”的概率.
如图，方格纸中有三个点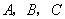
，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的顶点上．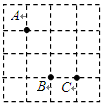
（1）在图甲中作出的四边形是中心对称图形但不是轴对称图形；
（2）在图乙中作出的四边形是轴对称图形但不是中心对称图形；
（3）在图丙中作出的四边形既是轴对称图形又是中心对称图形．
（注：图甲、图乙、图丙在答题纸上）
如图，在Rt△ABC中，∠C＝90°，O是斜边AB上的中点，AE=CE，BF∥AC.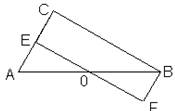
(1)求证：△AOE≌△BOF；
(2)求证：四边形BCEF是矩形.
如图，抛物线与x轴相交于B，C两点，与y轴相交于点A，P（2a，－4a2＋7a＋2）（a是实数）在抛物线上，直线y=k x +b经过A，B两点．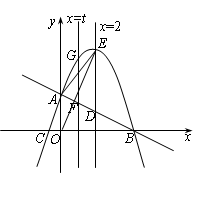
（1）求直线AB的解析式；
（2）平行于y轴的直线x=2交直线AB于点D，交抛物线于点E．
①直线x=t（0≤t≤4）与直线AB相交F，与抛物线相交于点G．若FG∶DE＝3∶4，求t的值；
②将抛物线向上平移m(m＞0)个单位，当EO平分∠AED时，求m的值．
如图，矩形ABCD中，AB="10" cm，BC="6" cm．现有两个动点P，Q分别从A，B同时出发，点P在线段AB上沿AB方向作匀速运动，点Q在线段BC上沿BC方向作匀速运动，已知点P的运动速度为1 cm/s，运动时间为t s．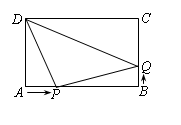
（1）设点Q的运动速度为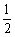
cm/s．
①当△DPQ的面积最小时，求t的值；
②当△DAP∽△QBP相似时，求t的值．
（2）设点Q的运动速度为a cm/s，问是否存在a的值，使得△DAP与△PBQ和△QCD这两个三角形都相似？若存在，请求出a的值；若不存在，请说明理由．