如图,抛物线经过原点 ,点 ,点 .
(1)求抛物线解析式;
(2)连接 ,过点 作 交抛物线于 ,连接 ,求 的面积;
(3)点 是 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 .问:是否存在点 ,使以点 , , 为顶点的三角形与(2)中的 相似,若存在,求出点 的坐标;若不存在,说明理由.

如图,已知AB是⊙O的直径.弦AC∥OD,求证:弧BD=弧CD.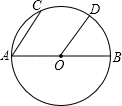
如图,AB是⊙O的直径,点C、D在圆上,且 =
= .
.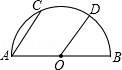
(1)求证:AC∥OD.
(2)若∠AOD=110°,求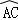 的度数.
的度数.
如图,已知AD是⊙O的直径,AD垂直于弦BC,垂足为点E.AB=AC吗?为什么?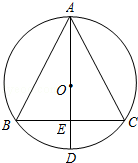
已知:如图,M是弧AB的中点,过点M的弦MN交弦AB于点C,设⊙O的半径为4cm,MN=4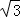 cm.
cm.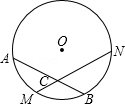
(1)求圆心O到弦MN的距离;
(2)猜想OM和AB的位置关系,并说明理由;
(3)求∠ACM的度数.
如图,⊙O的半径为17cm,弦AB=30cm.
(1)求圆心O到弦AB的距离;
(2)若⊙O中另有一条CD=16cm,且CD∥AB,求AB和CD间的距离.