阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数 、 的算术平均数, 叫做正数 、 的几何平均数,它是解决最大(小 值问题的有力工具.
例如:在 的条件下,当 为何值时, 有最小值,最小值是多少?
解: , 即是
当且仅当 即 时, 有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若 ,函数 ,当 为何值时,函数有最值,并求出其最值.
(2)当 时,式子 成立吗?请说明理由.
一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).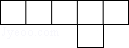
2015秋•永登县期末)为响应国家要求中小学生每天锻练1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.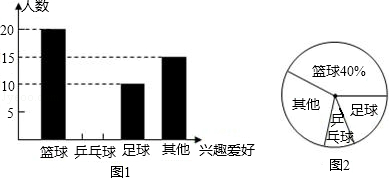
(1)求被调查的班级的学生人数;
(2)求喜欢“乒乓球”的学生人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)若该校共有2000名学生,请估计喜欢“足球”的学生人数.
解方程:
(1)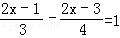
(2)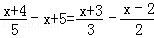 .
.
当 时,求代数式3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
时,求代数式3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.