如图,直角△ABC中,∠C=90°,AB=2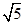 ,sinB=
,sinB=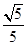 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.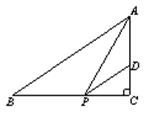
(1)求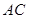 、
、 的长;
的长;
(2)设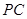 的长为
的长为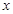 ,
, 的面积为
的面积为 .当
.当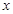 为何值时,
为何值时, 最大并求出最大值.
最大并求出最大值.
已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,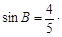

求:(1)线段DC的长;
(2)tan∠EDC的值.
已知二次函数y=-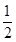 x2-x
x2-x .
.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
已知抛物线y=x2-2kx+3k+4.
(1)顶点在y轴上时,k的值为_________.
(2)顶点在x轴上时,k的值为_________.
(3)抛物线经过原点时,k的值为_______.
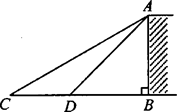
如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进(9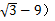 m到达D处,在D处测得建筑物顶端A的仰角为45°,求该建筑物AB的高度
m到达D处,在D处测得建筑物顶端A的仰角为45°,求该建筑物AB的高度