我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究:
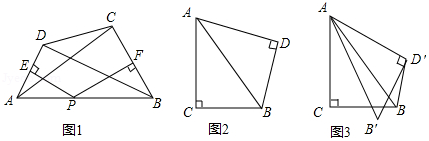
如图1,在等邻角四边形 中, , , 的中垂线恰好交于 边上一点 ,连接 , ,试探究 与 的数量关系,并说明理由;
(3)应用拓展:
如图2,在 与 中, , , ,将 绕着点 顺时针旋转角 得到 △ (如图 ,当凸四边形 为等邻角四边形时,求出它的面积.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
当x满足不等式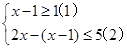 时,求方程
时,求方程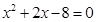 的解。
的解。
如图,已知线段AB.
(1)用尺规作图的方法作出线段AB的垂直平分线CD(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线CD上任意取两点M,N(线段AB的上方).连结AM,AN,BM,BN.求证:∠MAN=∠MBN.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.