在平面直角坐标系中,点 为原点,平行于 轴的直线与抛物线 相交于 , 两点(点 在第一象限),点 在 的延长线上.
(1)已知 ,点 的纵坐标为2.
①如图1,向右平移抛物线 使该抛物线过点 ,与 的延长线交于点 ,求 的长.
②如图2,若 ,过点 , 的抛物线 ,其顶点 在 轴上,求该抛物线的函数表达式.
(2)如图3,若 ,过 , , 三点的抛物线 ,顶点为 ,对应函数的二次项系数为 ,过点 作 轴,交抛物线 于 , 两点,求 的值,并直接写出 的值.

先化简,再求代数式
的值,其中x= cos300+
cos300+
已知半径为1cm的圆,在下面三个图中AC=10cm,AB=6cm,BC=8cm,在图2中∠ABC=90°.
(1)如图1,若将圆心由点A沿A C方向运动到点C,求圆扫过的区域面积;
C方向运动到点C,求圆扫过的区域面积;
(2)如图2,若将圆心由点A沿A B
B C方向运动到点C,求圆扫过的区域面积;
C方向运动到点C,求圆扫过的区域面积;
(3)如图3,若将圆心由点A沿A B
B C
C A方向运动回到点A.
A方向运动回到点A.
则I)阴影部分面积为____;Ⅱ)圆扫过的区域面积为____.
在直角坐标系中,C(2,3),C′(-4,3), C″(2,1),D(-4,1),A(0,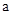 ),B(
),B(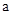 ,O)(
,O)( 
 0).
0).
(1)结合坐标系用坐标填空.
点C与C′关于点对称; 点C与C″关于点对称;点C与D关于点对称
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求 值.
值.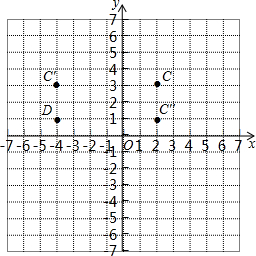
已知等边△ABC的边长为3个单位,若点P由A出发,以每秒1个单位的速度在三角形的边上沿A B
B C
C A方向运动,第一次回到点A处停止运动,设AP=S,用
A方向运动,第一次回到点A处停止运动,设AP=S,用 表示运动时间.
表示运动时间.
(1)当点P由B到C运动的过程中,用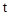 表示S;
表示S;
(2)当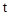 取何值时,S等于
取何值时,S等于 (求出所有的
(求出所有的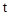 值);
值);
(3)根据(2)中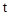 的取值,直接写出在哪些时段AP
的取值,直接写出在哪些时段AP ?
?
甲乙两单位随机选派相同人数参加科普知识比赛;每人得分成绩只有70分、80分、90分三种结果中一种,已知两单位得80分的人数相同,根据下列统计图回答问题.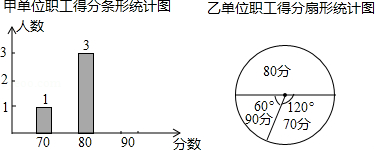
(1)求甲单位得90分的人数,将甲单位职工得分条形统计图补充完整;
(2)分别计算两个单位职工参加比赛成绩的平均分,由此你能估计出哪个单位职工对此次科普知识掌握较好,并说明理由;
(3)现从甲单位得80分和90分的人中任选两个人,列出所有的选取结果,并求两人得分不同的概率(用大写字母代表得90分的人,小写字母代表得80分的人).