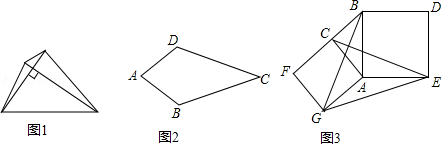
如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形 两组对边 , 与 , 之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 , , ,已知 , ,求 长.
(本题12分)一列快车从甲地驶往乙地,一列慢车从乙地 驶往甲地,两车同时出发,设慢车行驶的时间为
驶往甲地,两车同时出发,设慢车行驶的时间为 ,两车之间的距离为
,两车之间的距离为 ,图中的折线表示
,图中的折线表示 与
与 之间的函数关系.
之间的函数关系.
根据图象进行以下探究:(1)甲、乙两地之间的距离为
 km;
km;(2)请解释图中点
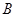 的实际意义;
的实际意义;(3)求慢车和快车的速度;
(4)求线段
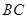 所表示的
所表示的 与
与 之间的函数关系式,并
之间的函数关系式,并
 写出自变量
写出自变量 的取值范围;
的取值范围;(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(本题10分)如图,已知在等腰直角三角形 中,
中,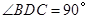 ,
, 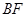 平分
平分 ,与
,与 相交于点
相交于点 ,延长
,延长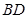 到
到 ,使
,使 ,
,
(1)试说明:
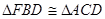 ;
;(2)延长
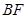 交
交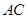 于
于 ,且
,且 ,)试说明:
,)试说明: ;
;(3)在⑵的条件下,若
 是
是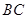 边的中点,连结
边的中点,连结 与
与 相交于点
相交于点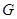 .
.
试探索 ,
, ,
, 之间的数量关系,并说明理由
之间的数量关系,并说明理由
(本题10分)为美化萧山,创建文明城市.园林部门决定利用现有的3600盆甲种花卉和2900盆 乙种花卉搭配A、B两种园艺造型共50个,
乙种花卉搭配A、B两种园艺造型共50个, 摆放在人民广场两侧,搭配每个造型所需花卉情况如下表所示
摆放在人民广场两侧,搭配每个造型所需花卉情况如下表所示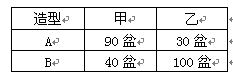
综合上述信息,解答下列问题:(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A型造型的成本为1000元,
搭配一个B型造型的成本为1200元.试说明运用(1)中哪种方案成本最低?
(本题8分)
某校八年级200名女生在体育测试中进行了立定跳远的测试.现从200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)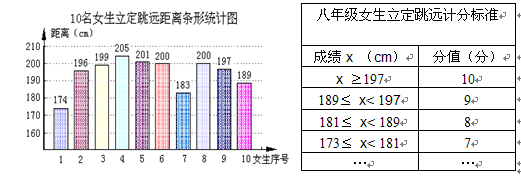
(1)求这10名女生立定跳远距离的中位数,立定跳远得分的众数和平均数.
(2)请你估计该校200名女生在立定跳远测试中得10分的人数.
(本小题满分8分)已知y – 2与x成正比例关系,且当x=1时,y=5.
(1)求
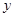 与
与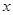 之间的函数解析式;
之间的函数解析式;(2)画出这个函数的图像,并求出该图像与坐标轴围成的三角形的面积。.