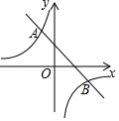
如图,一次函数 与反比例函数 的图象交于点 , .
(1)求这两个函数的表达式;
(2)在 轴上是否存在点 , ,使 为等腰三角形?若存在,求 的值;若不存在,说明理由.
已知矩形纸片ABCD中,AB=24厘米,BC=10厘米.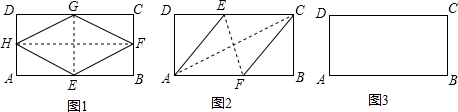
(1)按如下操作:先将矩形纸片上下对折,而后左右对折,再沿对角线对折,而后展开得到图中的折痕四边形EFGH(如图1),求菱形EFGH的面积.
(2)如图2,将矩形纸片ABCD折叠,使点A与点C重合得折痕EF,则四边形AECF必为菱形,请加以证明.
(3)请通过一定的操作,构造一个菱形EFGH(不同于第(1)题中的特殊图形),使菱形的四个顶点分别落在矩形ABCD的四条边上(E、F、G、H分别在边AB、BC、CD、DA上,且不与矩形ABCD的顶点重合).
①请简述操作的方法,并在图3中画出菱形EFGH.
②求菱形EFGH的面积的取值范围.
如图①,直线l:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B 两点,将△AOB绕点O逆时针旋转90°,得到△COD,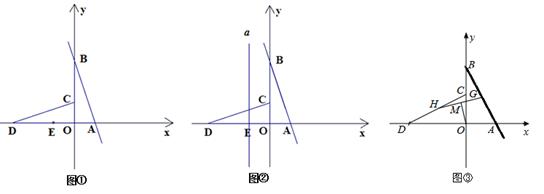
(1)若l: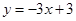 ,E为AD的中点,
,E为AD的中点,
①在CD上有一动点F ,求当△DEF与△COD相似时点F的坐标;
②如图②,过E作x轴的垂线a,在直线a上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点坐标;若不存在,请说明理由
(2)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=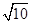 ,直接写出l的函数解析式.
,直接写出l的函数解析式.
九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) |
1≤x<50 |
50≤x≤90 |
| 售价(元/件) |
x+40 |
90 |
| 每天销量(件) |
200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
为了考察冰川融化的状况,一支科考队在某冰川上设定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.
小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长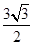 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.