如图，某日的钱塘江观潮信息如图：
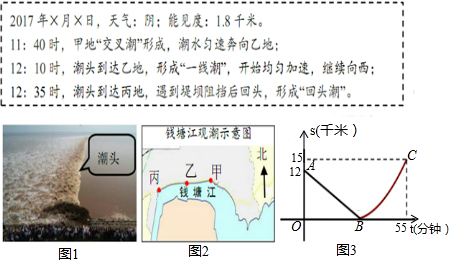
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离 （千米）与时间 （分钟）的函数关系用图3表示，其中：“ 时甲地‘交叉潮’的潮头离乙地12千米”记为点 ，点 坐标为 ，曲线 可用二次函数 ， 是常数）刻画．
（1）求 的值，并求出潮头从甲地到乙地的速度；
（2） 时，小红骑单车从乙地出发，沿江边公路以0.48千米 分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？
（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米 分，小红逐渐落后．问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度 ， 是加速前的速度）．
(本题满分8分)先化简，再求值：（
）÷a，其中a=
.
如图，数轴上有三个点A、B、C，它们可以沿着数轴左右移动，请回答：
（1）将点B向右移动三个单位长度后到达点D，点D表示的数是;
（2）移动点A到达点E，使B、C、E三点的其中任意一点为连接另外两点之间
线段的中点，请你直接写出所有点A移动的距离和方向；
（3）若A、B、C三个点移动后得到三个互不相等的有理数，它们既可以表示为
1，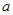
，
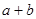的形式，又可以表示为0，
，
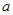的形式，试求，的值.
如图，一个用铝合金材料加工的长方形窗框，它的宽和高分别为
厘米，
厘米，解答下列问题（结果可用含，的代数式表示）．
（1）长方形窗框的面积是厘米2；
（2）铝合金窗分为上、下两栏，四周框架和中间隔栏的材料均为宽度6厘米的铝合金
材料，上栏和下栏的框内高度（不含铝合金部分）的比为1：2（接口用料忽略不计）.
①求制作一个该种窗框所需铝合金材料的总长度；
②求该种窗框的透光部分的面积.
直线AB、CD被直线EF所截，EF分别交AB、CD于M，N,∠EMB=50°,
MG平分∠BMF,MG交CD于G．
（1）如图1，若AB∥CD，求∠1的度数．
（2）如图2，若∠MNC=140°，求∠1的度数．
政府引导农民对生产的土特产进行加工后，分为甲、乙、丙三种不同包装
推向市场进行销售，其相关信息如下表：
| 重量（克/袋） |
销售价（元/袋） |
成本（元/袋） |
|
| 甲 |
400 |
4.8 |
3.8 |
| 乙 |
300 |
3.6 |
2.9 |
| 丙 |
200 |
2.5 |
1.9 |
这三种不同的包装的土特产都销售了120千克，那么本次销售中，那一种包装的
土特产获得的利润最大，最大利润是多少？