如图1，将 纸片沿中位线 折叠，使点 对称点 落在 边上，再将纸片分别沿等腰 和等腰 的底边上的高线 ， 折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．
（1）将 纸片按图2的方式折叠成一个叠合矩形 ，则操作形成的折痕分别是线段 ， ； ．
（2） 纸片还可以按图3的方式折叠成一个叠合矩形 ，若 ， ，求 的长；
（3）如图4，四边形 纸片满足 ， ， ， ， ，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并求出 、 的长．
画图并填空：
如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点C的对应点C′．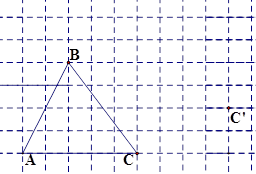
（1）画出平移后的△A′B′C′，（利用网格点和三角板画图）
（2）画出AB边上的高线CD；
（3）画出BC边上的中线AE；
（4）在平移过程中高CD扫过的面积为．（网格中，每一小格单位长度为1）
因式分解（本题满分6分，每小题2分）
（1）
；
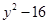（2）
；
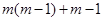（3）
；
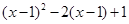计算（前3题，每题3分，第4题5分，共14分）
（1）
；
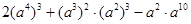（2）
；
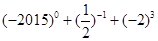（3）
；
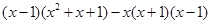（4）
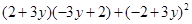；（本题先化简，再求值，其中
）
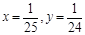如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．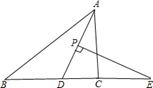
（1）若∠B=35°，∠ACB=85°，则∠E的度数=；
（2）当P点在线段AD上运动时，设∠B=α，∠ACB=β（β＞α），则∠E=．（用α，β的代数式表示）
（本题8分）如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC．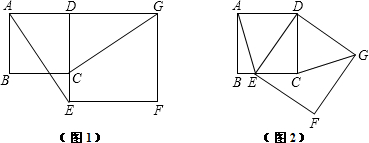
（1）试猜想AE与GC有怎样的位置关系，并证明你的结论；
（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC．你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．