问题背景
如图1,在正方形 的内部,作 ,根据三角形全等的条件,易得 ,从而得到四边形 是正方形.
类比探究
如图2,在正 的内部,作 , , , 两两相交于 , , 三点 , , 三点不重合)

(1) , , 是否全等?如果是,请选择其中一对进行证明.
(2) 是否为正三角形?请说明理由.
(3)进一步探究发现, 的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系.
如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、E.连接DE,CD,DE与BC相交于点G.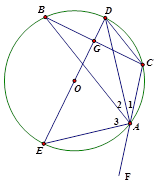
(1)求证:DE是△ABC的外接圆的直径.
(2)设OG=3,CD=2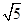 ,求⊙O的半径.
,求⊙O的半径.
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。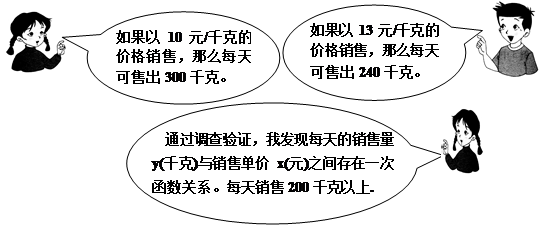
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式。
(2)该超市销售这种水果每天获取的利润为1040元,那么销售单价为多少元?
下图是单位长度为1的正方形网格,点A、B、C都在格点上;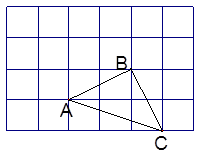
(1)画出将图中的△ABC绕点A逆时针旋转90°的△AB’C’ ,(其中B、C的对应点分别是
B’、C’)
(2)求(1)中点B在运动过程中所经过的弧长.
(3)求(1)中边AC在运动过程中所扫过的区域的面积.
如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°,以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;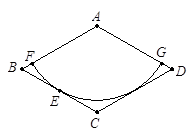
(1)请你判断所作的扇形与边CD的位置关系,并说明理由;
(2)若以所作出的扇形为侧面围成一个圆锥,求该圆锥的全面积.
已知关于x的一元二次方程x2 + mx +n+1=0的一根为2.
(1)用m的代数式表示n;
(2)求证:关于y的一元二次方程y2 +my+n=0总有两个不相等的实数根。