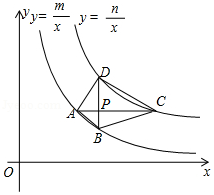
如图，四边形 的四个顶点分别在反比例函数 与 的图象上，对角线 轴，且 于点 ．已知点 的横坐标为4．
（1）当 ， 时．
①若点 的纵坐标为2，求直线 的函数表达式．
②若点 是 的中点，试判断四边形 的形状，并说明理由．
（2）四边形 能否成为正方形？若能，求此时 ， 之间的数量关系；若不能，试说明理由．
计算：
在正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②联结三个格点，使之构成直角三角形，小华在左边的正方形网格中作出了Rt△ABC，请求出斜边AC的长．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，使三个网格中的直角三角形互不全等，并分别求出这三个直角三角形的斜边长．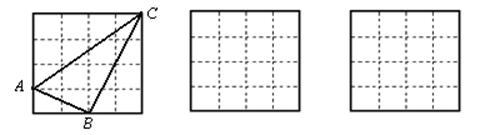
如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，求线段CN的长．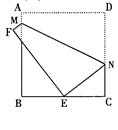
某水果店以每千克2元的价格新进一批水果，在市场销售中发现：此种水果的日销售量y（单位：千克）是销售单价x（单位：元/千克）的反比例函数，且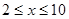
．已知当销售单价定为3元/千克时，日销售量恰好为40千克．
（1） 求出y与x的函数关系式；
（2） 为了避免该水果库存的积压，水果店经理确定了日销售量不少于20千克且日销售利润不低于60元的销售方案，求出此时销售单价的范围．
解：
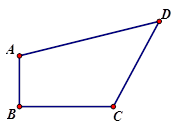
已知，如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积。