为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查.结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
如图,一次函数图象与x轴交于点A,与y轴交于点B,与双曲线 的一支交于第二象限内一点C.
的一支交于第二象限内一点C.
(1) 求字母n的取值范围;
(2) 若A(4,0),B(0,2),求一次函数解析式;
(3) 在(2)的情况下,若∠COB=∠CAO,求n的值.
如图,AB为⊙O的直径,CD切⊙O于D,CD=AB,E为AB下方⊙O上一点,且

(1)求证:四边形ABCD是平行四边形(2)若⊙O半径为5,AE=8,求 的正切值
的正切值
在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形。小明有一副三角尺和一个量角器(如图所示).
(1)小明在这三件文具中任选一件,结果是轴对称图形的概率是▲.
(2)在这三件文具中随机取出两件则可以拼成轴对称图形的概率是多少?
(3)小明把A、B 两把尺的各任意一个角拼在一起(无缝隙不重叠)得到一个更大的角,请画树状图或列表说明这个角是钝角的概率是多少?
A、B、C三个工程队共修建一段长240km的公路,图中分别反映了每个工程队承包的工程比例及每月完成公路的进度.
(1)若B队9个月完成的工程量与A队6个月完成的工程量相同,求a的值;
(2)在(1)的条件下,三队同时开工完成承包工程,则完成全部工程需要多少时间?
如图,网格中每个小正方形的边长为1,请你认真观察图(1)的三个网格中阴影部分构成的图案,解答下列问题: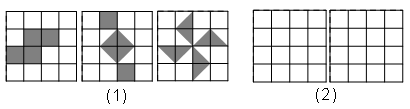
这三个图案都具有以下共同特征:都是▲对称图形,面积都是▲;
⑵ 请在图(2)中设计出2个具备上述特征而且不是轴对称图形的图案,要求所画图案不能
与图(1)中给出的图案相同.