阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为 的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想 转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程 ,可以通过因式分解把它转化为 ,解方程 和 ,可得方程 的解.
(1)问题:方程 的解是 , , ;
(2)拓展:用“转化”思想求方程 的解;
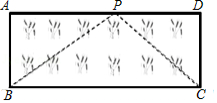
(3)应用:如图,已知矩形草坪 的长 ,宽 ,小华把一根长为 的绳子的一端固定在点 ,沿草坪边沿 , 走到点 处,把长绳 段拉直并固定在点 ,然后沿草坪边沿 、 走到点 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 .求 的长.
(本题10分)已知如图:点(1,3)在函数 (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数 (x>0)的图象又经过A、E两点,点E的横坐标为m.
(x>0)的图象又经过A、E两点,点E的横坐标为m.
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.
(本题10分)某超市如果将进货价为40元的商品按50元销售,就能卖出500个,但如果这种商品每个涨价1元,其销售量就减少10个,如果你是超市的经理,为了赚得8 000元的利润,你认为售价(售价不能超过进价的160%)应定为多少?这时应进货多少个?
(本题10分)阅读材料:分解因式:
解:
=
=
=
=
= ,
,
此种方法抓住了二次项和一次项的特点,然后加一项,使三项成为完全平方式,我们把这种分解因式的方法叫配方法.
(1)用上述方法分解因式: ;
;
(2)无论 取何值,代数式
取何值,代数式 总有一个最小值,请尝试用配方法求出当
总有一个最小值,请尝试用配方法求出当 取何值时代数式的值最小,并求出这个最小值.
取何值时代数式的值最小,并求出这个最小值.
(本题10分)在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,试判定四边形DEBF是何种特殊四边形?并说明理由.
(本题8分)已知,实数 ,
, ,
, 在数轴上的位置如图所示,化简:
在数轴上的位置如图所示,化简: .
.