如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 、 两点.动点 从点 出发,在线段 上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 关于点 的对称点为点 ,以线段 为边向上作正方形 .设运动时间为 秒.
(1)当 秒时,点 的坐标是 ;
(2)在运动过程中,设正方形 与 重叠部分的面积为 ,求 与 的函数表达式;
(3)若正方形 对角线的交点为 ,请直接写出在运动过程中 的最小值.

化简求值:[(x+y)(x-y)-(x-y)2+2y(x-y)]÷(-2y),其中x=- ,y=2.
,y=2.
分解因式:(x-y)2+4xy
分解因式:2x5-32x;
如图,直线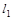 :
: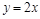 与直线
与直线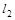 :
: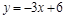 相交于点
相交于点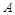 ,直线
,直线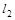 与
与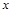 轴交于点
轴交于点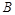 ,平行于
,平行于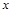 轴的直线
轴的直线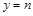 分别交直线
分别交直线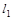 、直线
、直线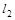 于
于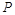 、
、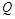 两点(点
两点(点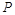 在
在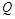 的左侧)
的左侧)
⑴点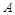 的坐标为;
的坐标为;
⑵如图1,若点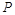 在线段
在线段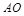 上,在
上,在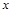 轴上是否存在一点
轴上是否存在一点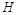 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点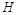 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶如图2.若以点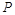 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角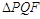 ,设
,设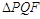 与
与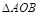 重叠部分的面积为
重叠部分的面积为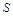 ,求
,求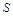 与
与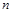 的函数关系式;并注明
的函数关系式;并注明 的取值范围.
的取值范围.
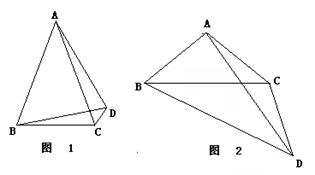
如图1,等腰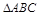 ,
, ,
,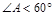 ,
,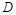 为
为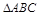 外部一点,在
外部一点,在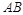 的右侧作
的右侧作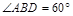 ,且
,且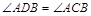
⑴探究线段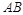 、
、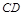 和
和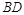 的数量关系;
的数量关系;
⑵若将“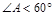 ”改为“
”改为“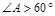 ”,⑴中的结论是否还成立?若成立,给出证明;若不成立,给出正确的结论,并简要说明理由.
”,⑴中的结论是否还成立?若成立,给出证明;若不成立,给出正确的结论,并简要说明理由.